refawebcam.blogg.se - Completing the square video tutorial

#Completing the square video tutorial how to#

Step 1: Find half of the coefficient of x.If the coefficient of x 2 is NOT 1, we will place the number outside as a common factor.

#Completing the square video tutorial how to#

Now that we have gone through the steps of completing the square in the above section, let us learn how to apply the completing the square method using an example.Įxample: Complete the square in the expression -4x 2 - 8x - 12.įirst, we should make sure that the coefficient of x 2 is '1'. How to Apply Completing the Square Method?

Step 5: Factorize the polynomial and apply the algebraic identity x 2 + 2xy + y 2 = (x + y) 2 (or) x 2 - 2xy + y 2 = (x - y) 2 to complete the square.

Step 4: Add and subtract the square obtained in step 2 to the x 2 term.

Step 3: Take the square of the number obtained in step 1.

Step 2: Determine half of the coefficient of x.

Step 1: Write the quadratic equation as x 2 + bx + c.

Given below is the process of completing the square stepwise: To apply the method of completing the square, we will follow a certain set of steps. But, how do we complete the square? Let us understand the concept in detail in the following sections. Since we have (x + m) whole squared, we say that we have "completed the square" here. In such cases, we write it in the form a(x + m) 2 + n by completing the square. X 2 + 2x + 3 cannot be factorized as we cannot find two numbers whose sum is 2 and whose product is 3. Let us have a look at the following example to understand this case.

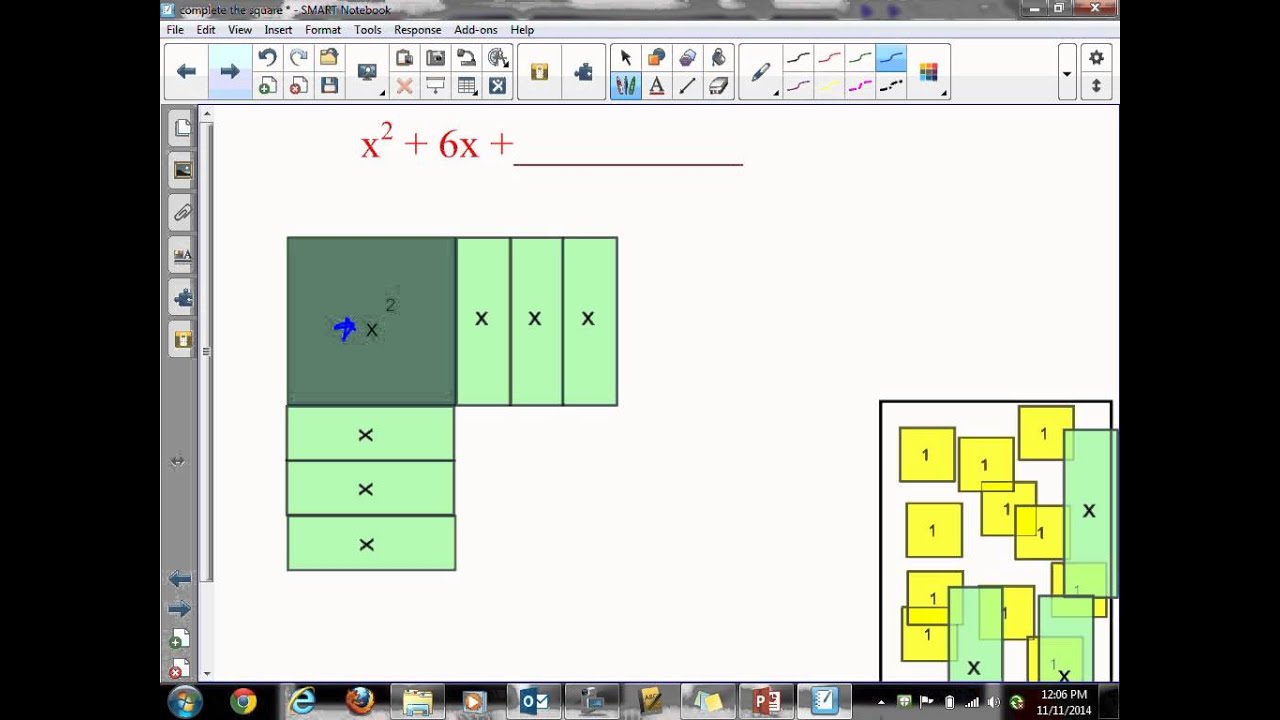
But sometimes, factorizing the quadratic expression ax 2 + bx + c is complex or NOT possible. We know that a quadratic equation of the form ax 2 + bx + c = 0 can be solved by the factorization method. The most common application of completing the square method is factorizing a quadratic equation, and henceforth finding the roots or zeros of a quadratic polynomial or a quadratic equation.